For advanced math problems, please have a look at the questions below.
Then study the examples and tips in the next section.
Follow the links for more free materials at the bottom of this page.
These excerpts are from our 400 Questions & Solutions -Math Download.
Advanced Math Problems
Instructions: Work out the solutions to the problems below. Then check your answers, which are provided in the next section.
1) What is the equivalent of the following logarithmic function in exponential form? 4 = log381
2) What number is next in the sequence? 2, 4, 16 . . .
3) What is the square root of -5?
4) What is x to the power of -6?
5) How many 2 letter combinations can be made from the letter set?:
H A N D Y
Answers to the Advanced Math Problems
1) 81 = 34
2) 256
3) an imaginary number
4) 1/x6
5) 10
Solutions to the Advanced Math Problems
Solution 1
1) Here we have the logarithmic function: 4 = log381
The above question is one of our trigonometric, logarithmic, or exponential function advanced math problems.
The logarithmic function x = logby is the same as y = bx in exponential form.
Remember x is for exponent and b is for base number in the above formula.
So 4 = log381 is the same as 81 = 34
Solution 2
2) What number is next in the sequence? 2, 4, 16 . . .
This is a series and sequences question.
For these problems, you have to discover the pattern that exists among of the numbers in the list provided.
In this series, each number is the previous number squared.
22 = 4
42 = 16
162 = 256
You may also see advanced math problems on how to calculate the nth item of a geometric sequence.
The first number in the sequence is represented by variable a and the multiplier (called the “common ratio”) is represented by variable r.
The formula for calculating the nth item in a geometric sequence is as follows: ar(n-1)
Solution 3
3) What is the square root of -25?
This is a question on imaginary numbers.
An imaginary number is the real number solution to the problem multiplied by the imaginary unit i.
The square root of 25 is 5, so our answer here is the imaginary number 5i.
Solution 4
4) What is x to the power of -6?
This is an advanced math problem on manipulating square roots and exponents.
When you see a negative number as an exponent, you need to express the result as a fraction.
The fraction will have 1 in the numerator and the given term with a positive exponent in the denominator.
So, x-6 = 1/x6
Solution 5
5) You may have questions on combinations or permutations on the test.
Our question was: How many 2 letter combinations can be made from the following 5 letter set? H A N D Y
Tip 1:
Remember that a combination, unlike a permutation, does not take into account the order of the items in the combination.
For example, the combination H A is considered the same as the combination A H.
To determine the number of combinations of S at a time that can be made from a set containing N items, you need this formula:
(N!) ÷ [(N − S)! × S!]
Remember: S represents how many letters each combination should contain. Each combination will contain 2 letters in this exercise, so S = 2.
N represents total set (H A N D Y in this example). So, N = 5 because there are five letters in the set.
So in the example above, S = 2 and N = 5
Here is the formula again: (N!) ÷ [(N − S)! × S!]
Tip 2:
The exclamation point is a factorial.
For factorials, you have to multiply the stated number by every number less than it. For example, 5! = 5 × 4 × 3 × 2 × 1
Now substitute the values for S and N and carry out the operation represented by the exclamation point:
(5 × 4 × 3 × 2 × 1) ÷ [(5 − 2)! × 2!] =
(5 × 4 × 3 × 2) ÷ [(3 × 2 × 1) × (2 × 1)] =
120 ÷ (6 × 2) =
120 ÷ 12 = 10
So 10 two-letter combinations can be made from a five letter set.
Permuations
Permutations are like combinations, except permutations take into account the order of the items in each group.
For permutations of S at a time from a set containing N items, use the formula: N! ÷ (N – S)!
More Advanced Math
You may also see questions like these on the advanced math problems section of your exam.
What ordered pair is a solution to the following system of equations?
x + y = 12
xy = 35
This is a systems of equations problem.
Questions in this skill set will include operations with imaginary numbers.
In the standard (x,y) plane, what is the distance between (3, 4) and (6, 2)?
HINT: If the problem is asking you about points on a plane, for instance, you will need to use the distance formula.
This problem is classified as geometry: graphs, coordinates, slope, lines, cones, and sets of points on a plane.
So, a math question on this part of the examination would be similar to this one.
Simplify the following:
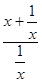
This is a problem on simplifying rational expressions.
It is an example of a simplification problem, containing fractions within fractions, like you will see on the test.
Get the Math Download
The questions on this page are samples from our math download.
The math download shows you how to solve the toughest math problems.
19 Accuplacer Practice Tests – PDF
Advanced math problems on your college entrance test will include topics that you may have studied in an advanced math course in high school.
The problems in each of the math sections of the Accuplacer consist of twenty questions each.
Get More Accuplacer Help
You may also wish to have a look at our other advanced math problems and exercises:
