Accuplacer Math Prep – 50 Problems with Answers & Explanations
The Accuplacer math prep problems on this page are up-to-date for the new exam.
Instructions: There are fifty Accuplacer math prep problems on this page. The math problems are grouped into sets of five. You can complete the all of the practice problems in one sitting, or check your answers at the end of each set. You can also try the other materials below.
Math PDF Download with 400 Problems
The questions in this Accuplacer math practice test are ordered from basic to advanced.
So, we recommend that you complete the practice problems in the order provided.
Accuplacer Math Prep – Questions 1 to 5
1) a3 × a4 = ?
2) (y2)4 = ?
3) Simplify, then state whether the result is a rational or irrational number:
3 × 5 × π
4) Simplify, then state whether the result is a rational or irrational number:
$ \sqrt{3} \times \sqrt{3}$
5) 3 + 150 ÷ 6 ÷ 2 × 4 – 8 = ?
Go to the answers for questions 1 to 5
Accuplacer Math Prep – Questions 6 to 10
Before competing exercises 6 and 7, you may want to view more information on perfect squares.
6) x2 – y2
7) 2a2 – 98b2
8) Solve for x and y if 3x + y = 20 and 2x + 2y = 16. Use the substitution method.
9) Group like terms together and then factor: ab2y – 3a + 9b2y – 27
10) 3 is added to the original value, then 5 is subtracted from this sum to get 68.
What is the original value?
Go to the answers for questions 6 to 10
Accuplacer Math Prep – Questions 11 to 15
11) Factor: 18a2b3c + 12a3b2c2 – 24ab4c3
12) Simplify:
$ \dfrac{3x – 5}{2} = 10$
13) Simplify:
If | x + y | = 5 and x = 3, then what are the possible value of y ?
14) Identify the variables, the coefficients, and the constant in the expression below.
4a2 + 16ab + 24b4 – 8
15) Factor: a2b3c2 + a3b4c2 + ab2c
Go to the answers for questions 11 to 15
Accuplacer Math Prep – Questions 16 to 20
16) Find the greatest common factor:
100x4y – 300x3y2 + 400x2y2 – 200
17) Factor: 5b + 25c
18) Which of the following are monomials?
14
15b + ab
3xy
43xy + x + y
25x2
19) Balance the equation and express your answer as a simplified fraction, if possible.
If A + B – C = D, then A = ?
20) Group like terms and simplify:
(6x2 + 9xy + 7y2) + (8x2 + 2xy + 5y2) = ?
Go to the answers for questions 16 to 20
Accuplacer Math Prep – Questions 21 to 25
21) Solve for a:
3a + 8 = 4a – 2
22) Simplify:
$ \sqrt{196} = ? $
23) Simplify:
$ \sqrt{121} = ? $
24) Perform the operation:
(5x2 – 3xy + 4y2) – (2x2 + 9xy – 7y2) = ?
25) Factor: 9a –3b + 15c2
Go to the answers for questions 21 to 25
Accuplacer Math Prep – Questions 26 to 30
26) (16x3 + 8x2 + 4x) ÷ (2x) = ?
27) Solve for a and b using the elimination method:
3a + 5b = 4
2a – b = 7
28) Simplify:
$latex \sqrt{7} \times \sqrt{13}$
29) Simplify:
$ \sqrt[3]{\dfrac{216}{343}} = ?$
30) Simplify:
10x + 5y – 6x + 12 + 3y – 6
Go to the answers for questions 26 to 30
Questions 31 to 35
31) Use the FOIL method to simplify: (3x – 2)2
32) Use the FOIL method to simplify: (5a – 1)(3a + 9)
33) Expand by multiplying polynomials: a2b2(2a2b + 3a3b3)
34) Expand by multiplying polynomials: x3y3(4x3y2 + 5x2y2)
35) Which of the following are rational numbers:
24/72
$ \dfrac{\pi}{\sqrt{16}}$
$ \dfrac{\sqrt{3} – 1}{-2}$
Go to the answers for questions 31 to 35
Questions 36 to 40
36) Express in scientific notation: 19,875.246
37) Represent the solution to the following on a number line:
3x < –6
38) Find all possible values of x for the inequality:
x2 – 4x < 5
39) Use the elimination method to solve the system of equations:
Solve for x and y if x = y + 7 and x + y – 1 = 10
40) Factor: a3 – 273
Go to the answers for questions 36 to 40
Questions 41 to 45
41) Rewrite in the form ax2 ± bx ± c = 0. Then solve for x.
3x2 – 6x + 0 = 0
42) Rewrite in the form ax2 ± bx ± c = 0. Then solve for x.
2x2 + 3x = 65
43) Find the possible solutions for the quadratic equation:
(x + 9)(x + 4) = 0
44) Find the possible solutions for the quadratic equation:
(x – 2)(x + 5) = 0
45) Factor the following quadratic equation:
x2 + 5x + 6 = 0
Go to the answers for questions 41 to 45
Questions 46 to 50
For questions 46 and 47, identify which of the equations are quadratic equations, giving the reason for your answer.
Then re-write those equations into the standard quadratic equation format, using variables b and c where necessary.
46) 5x + 3 = 3x
47) 2x2 = 50
48) Use the quadratic formula to solve for x: x2 + 13x +36 = 0
49) Use the remainder theorem to find the remainder in the following problem:
x3 + 4x2 – 5x – 18 ÷ (x + 4)
50) Re-write the following quadratic equation in the completed square form. Then solve for x.
x2 + 6x + 4 = 0
Go to the answers for questions 46 to 50
Math Problems – Answers 1 to 5
Answer 1
The correct answer is: a7
For algebra problems like this one, you need to understand the laws of exponents.
a3 × a4 = a3 + 4 = a7
Answer 2
The correct answer is: y8
If you have problems with algebra questions on exponents, study these exponent laws.
(y2)4 = y2 x 4 = y8
Answer 3
The correct answer is: irrational
Click on these links for further practice with algebra problems on rational numbers and irrational numbers.
15π is an irrational number.
When π is multiplied by a rational number like 15, the result is irrational.
It is irrational because π has an infinite number of decimal places.
Any number multiplied by π has an infinite number of decimal places.
Answer 4
The correct answer is: rational
When simplified, we get 3, which is a rational number.
$latex \sqrt{3} \times \sqrt{3} =$
$latex \sqrt{3}^2 = 3$
Answer 5
The correct answer is: 45
To solve algebra equations like this one, you should study PEMDAS – Order of Operations.
There are no parentheses or exponents.
Do the multiplication and division from left to right.
3 + 150 ÷ 6 ÷ 2 × 4 – 8 =
3 + (150 ÷ 6) ÷ 2 × 4 – 8 =
3 + 25 ÷ 2 × 4 – 8 =
3 + (25 ÷ 2) × 4 – 8 =
3 + 12.5 × 4 – 8 =
3 + (12.5 × 4) – 8 =
3 + 50 – 8
Then do the addition and subtraction from left to right.
3 + 50 – 8 =
53 – 8 = 45
Go to question 6
Math Problems – Answers 6 to 10
Answer 6
The correct answer is: (x + y)(x – y)
For Accuplacer math prep problems like questions 6 and 7, you may need to review perfect squares.
You should know from memory that x2 – y2 = (x + y)(x – y).
Answer 7
The correct answer is: 2(a + 7b)(a – 7b)
2a2 – 98b2 =
2(a2 – 49b2) =
2(a + 7b)(a – 7b)
Answer 8
The correct answer is: x = 6 and y = 2
To solve algebra questions like this one, you can use the substitution method.
Step 1: Label the equations
Our equations were 3x + y = 20 and 2x + 2y = 16.
Label the equations A and B:
(A) 3x + y = 20
(B) 2x + 2y = 16
Step 2: Isolate one of the variables
We will isolate variable y in equation A in this solution.
Equation A is 3x + y = 20.
Perform inverse operations to isolate y.
3x + y = 20
3x – 3x + y = 20 – 3x
3x – 3x + y = 20 – 3x
y = 20 – 3x
Step 3: Substitute the value of the isolated variable
We have just determined that y = 20 – 3x.
Equation B is 2x + 2y = 16.
So, we will substitute 20 – 3x for the value of y in equation B.
2x + 2y = 16
2x + 2(20 – 3x) = 16
Step 4: Then perform the multiplication
2x + 2(20 – 3x) = 16
2x + (2 × 20) – (2 × 3x) = 16
2x + 40 – 6x = 16
Step 5: Perform inverse operations to solve for x
2x + 40 – 6x = 16
2x + 40 – 40 – 6x = 16 – 40
2x + 40 – 40 – 6x = 16 – 40
2x – 6x = 16 – 40
2x – 6x = –24
–4x = –24
–4x ÷ –4 = –24 ÷ –4
x = 6
Step 6: Substitute the value of x to solve for y
We have just determined that x = 6.
Equation B is 2x + 2y = 16.
2x + 2y = 16
(2 × 6) + 2y = 16
12 + 2y = 16
12 – 12 + 2y = 16 – 12
12 – 12 + 2y = 16 – 12
2y = 16 – 12
2y = 4
2y ÷ 2 = 4 ÷ 2
y = 2
Answer 9
The correct answer is: (b2y – 3)(a + 9)
To find the solution to Accuplacer math prep problems such as this, you need to group like terms together and then factor.
ab2y – 3a + 9b2y – 27 =
(ab2y – 3a) + (9b2y – 27) =
[(a × b2 × y) – (3 × a)] + [(9 × b2 × y) – (9 × 3)] =
[(a × b2 × y) – (a × 3)] + [(9 × b2 × y) – (9 × 3)] =
a[(a × b2 × y) – (a × 3)] + 9[(9 × b2 × y) – (9 × 3)] =
a[(b2 × y) – (3)] + 9[((b2 × y) – (3)] =
a(b2y – 3) + 9(b2y – 3) =
(b2y – 3)[a(b2y – 3) + 9(b2y – 3)] =
(b2y – 3)(a + 9)
Answer 10
The correct answer is: 70
For algebra problems asking for the original value, you need to solve by using inverse operations.
Set up the equation: x + 3 – 5 = 68
Set up the inverse operation: 68 + 5 – 3 = x
Solve to get the original value: 68 + 5 – 3 = 73 – 3 = 70
Go to question 11
Math Problems – Answers 11 to 15
Answer 11
The correct answer is: 6ab2c(3ab + 2a2c – 4b2c2)
For help with algebra questions asking you to factor, you can study factoring quadratics.
18a2b3c + 12a3b2c2 – 24ab4c3 =
ab2c(18ab + 12a2c – 24b2c2) =
ab2c[(6 × 3)ab + (6 × 2)a2c – (6 × 4)b2c2] =
6ab2c(3ab + 2a2c – 4b2c2)
Answer 12
The correct answer is: x = 25/3
To learn how to solve Accuplacer math prep problems that ask you to simplify, have a look at simplifying expressions.
Eliminate the fraction by multiplying each side by the denominator.
$ \dfrac{3x – 5}{2} = 10$
$ \dfrac{3x – 5}{2} \times 2 = 10 \times 2$
3x – 5 = 20
Deal with the integer.
3x – 5 + 5 = 20 + 5
3x = 25
Divide by the coefficient to solve.
3x ÷ 3 = 25 ÷ 3
$ \text x = \dfrac{25}{3}$
Answer 13
The correct answer is: –8 = y = 2
To solve similar algebra questions on your exam, learn more about absolute value.
If | x + y | = 5 and x = 3, we can substitute 3 for the value of x to solve.
| x + y | = 5
| 3 + y | = 5
| 3 + 2 | = 5
y = 2
However, for absolute value problems, you also have to consider other possible values.
If | x + y | = 5 then | x + y | = | –5 |
We know this because the absolute value of –5 is 5.
So again substitute for the value of x to solve.
| x + y | = | –5 |
| 3 + y | = | –5 |
| 3 + –8 | = | –5 |
When dealing with a negative number, we have to reverse the way the inequality sign points.
y = –8
So, the possible value of y is:
–8 = y = 2
Answer 14
The correct answers are: the variable in the first term is a; the variables in the second term are a and b; the variable in the third term is b.
To answer these types of algebra equations, look at the page on algebraic terms.
The coefficient in the first term is 4. The coefficient in the second term is 16. The coefficient in the third term is 24.
The constant is –8.
Answer 15
The correct answer is: ab2c(abc + a2b2c + 1)
For algebra equations on factoring, you may want to have another look at how to factor quadratics.
a2b3c2 + a3b4c2 + ab2c =
(a × a × b × b × b × c × c) + (a × a × a × b × b × b × b × c × c) + (a × b × b × c) =
ab2c(a × a × b × b × b × c × c) + (a × a × a × b × b × b × b × c × c) + (a × b × b × c) =
ab2c[(a × b × c) + (a × a × b × b × c) + (1)] =
ab2c(abc) + (a2 × b2 × c) + (1)] =
ab2c(abc + a2b2c + 1)
Go to question 16
Math Problems – Answers 16 to 20
Answer 16
The correct answer is: 100
Click on the following link for help with Accuplacer math prep problems on how to find the greatest common factor.
The last term on this expression (200) does not contain any variables.
So, our greatest common factor consists of a number only.
100x4y – 300x3y2 + 400x2y2 – 200 =
(100 × 1)x4y – (100 × 3)x3y2 + (100 × 4)x2y2 – (100 × 2) =
100[(100 × 1)x4y – (100 × 3)x3y2 + (100 × 4)x2y2 – (100 × 2)] =
100(x4y – 33y2 + 4x2y2 – 2)
So, the greatest common factor is 100.
Answer 17
The correct answer is: 5(b + 5c)
For more algebra questions like this, view our posts on factoring.
5b + 25c =
(5 × b) + (25 × c) =
(5 × b) + (5 × 5 × c) =
5[(5 × b) + (5 × 5 × c)] =
5[(b) + (5 × c)] =
5(b + 5c)
Answer 18
The correct answers are: 4, 3xy and 25x2
For algebra problems like this one, you need to understand monomials.
Answer 19
The correct answer is: A = D + C – B
To solve algebra equations like the one below, you might like to study balancing equations again.
If A + B – C = D, then A = ?
A + B – C = D
A + B – C + C = D + C
A + B – C + C = D + C
A + B – B = D + C – B
A + B – B = D + C – B
A = D + C – B
Answer 20
The correct answer is: 14x2 + 11xy + 12y2
To learn how to solve these types of algebra equations, study our post on grouping like terms.
(6x2 + 9xy + 7y2) + (8x2 + 2xy + 5y2) =
6x2 + 9xy + 7y2 + 8x2 + 2xy + 5y2 =
6x2 + 8x2 + 9xy + 7y2 + 8x2 + 2xy + 5y2 =
6x2 + 8x2 + 9xy + 7y2 + 2xy + 5y2 =
6x2 + 8x2 + 9xy + 2xy + 7y2 + 2xy + 5y2 =
6x2 + 8x2 + 9xy + 2xy + 7y2 + 5y2 =
(6x2 + 8x2) + (9xy + 2xy) + (7y2 + 5y2) =
14x2 + 11xy + 12y2
Go to question 21
Math Problems – Answers 21 to 25
Answer 21
The correct answer is: a = 10
Click on the following link to learn how to solve algebraic equations for an unknown variable.
Deal with the constants.
3a + 8 = 4a – 2
3a + 8 + 2 = 4a – 2 + 2
3a + 8 + 2 = 4a – 2 + 2
3a + 10 = 4a
Then get the variable on one side of the equation.
3a + 10 = 4a
3a – 3a + 10 = 4a – 3a
3a – 3a + 10 = 4a – 3a
10 = a
a = 10
Answer 22
The correct answer is: 14
To solve algebra questions like 22 and 23, you need to memorize the perfect squares.
196 is a perfect square.
$latex \sqrt{196} = 14 $
Answer 23
The correct answer is: 11
121 is a perfect square.
$ \sqrt{121} = 11 $
Answer 24
The correct answer is: 3x2 – 12xy + 11y2
To find the solutions for algebra equations like this one, learn how to subtract polynomials.
(5x2 – 3xy + 4y2) – (2x2 + 9xy – 7y2) =
5x2 – 3xy + 4y2 – 2x2 – 9xy – –7y2 =
5x2 – 3xy + 4y2 – 2x2 – 9xy + 7y2 =
5x2 – 2x2 – 3xy + 4y2 – 2x2 – 9xy + 7y2 =
5x2 – 2x2 – 3xy + 4y2 – 9xy + 7y2 =
5x2 – 2x2 – 3xy – 9xy + 4y2 – 9xy + 7y2 =
5x2 – 2x2 – 3xy – 9xy + 4y2 + 7y2 =
(5x2 – 2x2) + (–3xy – 9xy) + (4y2 + 7y2) =
3x2 + –12xy + 11y2 =
3x2 – 12xy + 11y2
Answer 25
The correct answer is: 3(3a – b + 5c2)
Click on this link for help with Accuplacer math prep questions on factoring.
9a –3b + 15c2 =
(3 × 3)a – (3 × 1)b + (3 × 5)c2 =
3(3a – b + 5c2)
Go to question 26
Math Problems – Answers 26 to 30
Answer 26
The correct answer is: 8x2 + 4x + 2
Get help with Accuplacer math prep questions like this on dividing polynomials.
(16x3 + 8x2 + 4x) ÷ (2x) =
(16x3 ÷ 2x) + (8x2 ÷ 2x) + (4x ÷ 2x) =
(16x3 ÷ 2x) + (8x2 ÷ 2x) + (2) =
(16x3 ÷ 2x) + (4x) + 2 =
8x2 + 4x + 2
Answer 27
The correct answer is: a = 3 and b = –1
To solve algebra problems like this, you need to learn the elimination method.
Our algebra equations were:
3a + 5b = 4
2a – b = 7
Multiply the second equation by 5.
2a – b = 7
(2a × 5) – (b × 5) = (7 × 5)
10a – 5b = 35
Now perform the elimination method by adding this to the first equation.
3a + 5b = 4
+ 10a – 5b = 35
13a = 39
13a ÷ 13 = 39 ÷ 13
a = 3
Now substitute the value of a to solve for b.
a = 3
2a – b = 7
(2 × 3) – b = 7
6 – b = 7
6 – b + b = 7 + b
6 – b + b = 7 + b
6 = 7 + b
6 – 7 = 7 – 7 + b
6 – 7 = 7 – 7 + b
6 – 7 = b
–1 = b
b = –1
Answer 28
The correct answer is: $latex \sqrt{91}$
Click on the following link for these types of algebra problems on radicals.
Solve as follows:
$ \sqrt{7} \times \sqrt{13} =$
$ \sqrt{7 \times 13} =$
$ \sqrt{91}$
Answer 29
The correct answer is: $latex \dfrac{6}{7}$
For algebra problems like this, you should memorize the perfect cubes.
Both 216 and 343 are perfect cubes.
Solve as follows:
$ \sqrt[3]{\dfrac{216}{343}} = $
$ \sqrt[3] {\dfrac{6 \times 6 \times 6}{7 \times 7 \times 7}} = $
$ \dfrac{6}{7}$
Answer 30
The correct answer is: 4x + 8y + 6
These types of Accuplacer math prep problems are asking you how to simplify algebraic expressions.
10x + 5y – 6x + 12 + 3y – 6 =
10x – 6x + 5y – 6x + 12 + 3y – 6 =
10x – 6x + 5y + 12 + 3y – 6 =
4x + 5y + 12 + 3y – 6 =
4x + 5y + 3y + 12 + 3y – 6 =
4x + 5y + 3y + 12 – 6 =
4x + 8y + 12 – 6 =
4x + 8y + 6
Go to question 31
Math Problems – Answers 31 to 35
Answer 31
The correct answer is: 9x2 – 12x + 4
For algebra equations like 31 and 32, you need to study the FOIL method.
(3x – 2)2 =
(3x – 2) × (3x – 2) =
(3x × 3x) + (3x × –2) + (–2 × 3x) + (–2 × –2) =
9x2 + –6x + –6x + 4 =
9x2 – 6x – 6x + 4 =
9x2 – 12x + 4
Answer 32
The correct answer is: 15a2 + 42a – 9
(5a – 1)(3a + 9) =
(5a × 3a) + (5a × 9) + (–1 × 3a) + (–1 × 9) =
15a2 + 45a + –3a + –9 =
15a2 + 45a – 3a – 9 =
15a2 + 42a – 9
Answer 33
The correct answer is: 3a5b5 + 2a4b3
For the algebra equations in questions 33 and 34, you need to multiply polynomials.
a2b2(2a2b + 3a3b3) =
(a2b2 × 2a2b) + (a2b2 × 3a3b3) =
2a4b3 + 3a5b5 =
3a5b5 + 2a4b3
Answer 34
The correct answer is: 4x6y5 + 5y5y5
x3y3(4x3y2 + 5x2y2) =
(x3y3 × 4x3y2) + (x3y3 × 5x2y2) =
4x6y5 + 5x5y5
Answer 35
The correct answer is: 24/72
For algebra problems like this one, you need to know how to identify rational numbers.
24/72 is rational because is a fraction. When simplified, it is a repeating decimal.
$ \dfrac{\pi}{\sqrt{16}}$
The above is not rational because p is a non-terminating decimal.
$ \dfrac{\sqrt{3} – 1}{-2}$
The above is not rational, even through the denominator has been rationalized. That is because the square root of 3 is a non-terminating decimal.
Go to question 36
Math Problems – Answers 36 to 40
Answer 36
The correct answer is: 1.9875246 × 104
To solve algebra problems like this, you should study scientific notation.
Remember that the number before the times sign has to be between 1 and 10.
We move the decimal four places to the left to get 1.9875246.
Since we have moved the decimal four places, we use 4 as our exponent:
1.9875246 × 104
Answer 37
The correct answer is: x > –2.
Also see the number line below.
To solve algebra problems such as this, you need to learn how to create number lines.
Solve for x first.
3x > –6
3x ÷ 3 > –6 ÷ 3
x > –6 ÷ 3
x > –2
Then represent the result on a number line.
You need to use an open dot because you do not have the equals to sign.
We have the “greater than” symbol, so the line needs to point to the right.
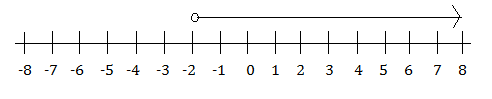
Answer 38
The correct answer is: –1 < x < 5
For algebra questions like this one, you need to study how to solve quadratic inequalities.
x2 – 4x < 5
x2 – 4x – 5 < 5 – 5
x2 – 4x – 5 < 0
(x + 1)(x – 5) < 0
(x + 1)(x – 5) < 0 ? x > –1
(x + 1)(x – 5) < 0 ? x < 5
–1 < x < 5
Answer 39
The correct answer is: x = 9 and y = 2
To solve these types of algebra equations, you should look at solving systems of equations.
x = y + 7
x + y – 1 = 10
Combine the two equations and solve for x.
x + x + y – 1 = y + 7 + 10
x + x + y – y – 1 = y – y + 7 + 10
x + x + y – y – 1 = y – y + 7 + 10
x + x – 1 = 7 + 10
x + x – 1 + 1 = 7 + 10 + 1
x + x – 1 + 1 = 7 + 10 + 1
x + x = 7 + 10 + 1
x + x = 18
2x = 18
2x ÷ 2 = 18 ÷ 2
x = 9
Then substitute the value of x into one of the original equations to solve for y.
x = 9
x = y + 7
9 = y + 7
9 – 7 = y + 7 – 7
9 – 7 = y + 7 – 7
9 – 7 = y
2 = y
y = 2
Answer 40
The correct answer is: (a – 3)(a2 + 3a + 9)
For algebra equations like this one, you need to factor quadratics.
a3 – 273 =
(a – 3)(a2 + 3a + 32) =
(a – 3)(a2 + 3a + 9)
Go to question 41
Math Problems – Answers 41 to 45
Answer 41
The correct answers are: 3x2 – 6x = 0 and (x = 0 or x = 2)
To solve Accuplacer math prep problems like questions 41 and 42 you need to understand the quadratic forms and know how to solve quadratic equations.
In this equation, c = 0.
The equation can be rewritten as follows:
3x2 – 6x + 0 = 0
3x2 – 6x = 0
(x = 0 or x = 2)
Answer 42
The correct answers are: 2x2 + 3x – 65 = 0 and (x = –6.5 or x = 5)
The equation can be rewritten as follows:
2x2 + 3x = 65
2x2 + 3x – 65 = 65 – 65
2x2 + 3x – 65 = 0
This is the standard quadratic form.
(x = –6.5 or x = 5)
Answer 43
The correct answers are: –9 and –4
For algebra problems like questions 43 and 44, you need to know how to solve quadratic equations.
(x + 9)(x + 4) = 0
(–9 + 9)(x + 4) = 0
(x + 9)(–4 + 4) = 0
So, the solutions are –9 and –4.
Answer 44
The correct answers are: 2 and –5
(x – 2)(x + 5) = 0
(2 – 2)(x + 5) = 0
(x – 2)(–5 + 5) = 0
So, the solutions are 2 and –5.
Answer 45
The correct answer is: (x + 2)(x + 3) = 0
To solve algebra problems like this, you might need help with factoring quadratics.
Our original equation was: x2 + 5x + 6 = 0
STEP 1: Look at the third term of the equation, which is 6.
Find two integers that equal 6 when multiplied.
1 × 6 = 6
2 × 3 = 6
–1 × –6 = 6
–2 × –3 = 6
STEP 2: Look at the second term of the equation, which is 5x.
Find two integers from step 1 that equal 5 when they are added.
2 + 3 = 5
STEP 3: Use the integers 2 and 3 to factor our quadratic.
(x + 2)(x + 3) = 0
Go to question 46
Math Problems – Answers 46 to 50
Answer 46
The correct answer is: not quadratic
For algebra problems like 46 and 47, you need to know the standard quadratic equation format.
Our equation was: 5x + 3 = 3x
The equation is not quadratic because it only has a variable raised to the power of one.
It does not have a variable that is raised to the power of 2.
Answer 47
The correct answer is: quadratic
Our equation was: 2x2 = 50
The equation is quadratic because it has a variable that is raised to the power of 2.
It can be re-written in the standard form as:
2x2 + bx – 50 = 0 (where b = 0)
(x = 5 or x = –5)
Answer 48
The correct answers are: –9 and –4
For advanced Accuplacer math prep problems like this one, study how to use the quadratic formula.
x2 + 13x + 36 = 0
a = 1 b = 13 c = 36
$ \text{x} = \dfrac{-b \pm \sqrt{b^{2} – 4ac}}{2a}$
$ \text{x} = \dfrac{-13 \pm \sqrt{13^{2} – (4 \times 1 \times 36)}}{2 \times 1}$
$ \text{x} = \dfrac{-13 \pm \sqrt{169 – 144}}{2}$
$ \text{x} = \dfrac{-13 \pm \sqrt{25}}{2}$
$ \text{x} = \dfrac{-13 \pm 5}{2}$
$ \text{x} = \dfrac{-13 – 5}{2} = \dfrac{-18}{2} = -9 $
$ \text{x} = \dfrac{-13 + 5}{2} = \dfrac{-8}{2} = -4 $
Answer 49
The correct answer is: remainder of 2
To answer this Accuplacer math prep problem, you need to study the remainder theorem.
Our question was: x3 + 4x2 – 5x – 18 ÷ (x + 4)
The opposite of the constant in the binomial is –4.
Replace x with –4 to use the remainder theorem to solve.
x3 + 4x2 – 5x – 18
–43 + (4 × –42) + (–5 × –4) + (–18) =
–64 + (4 × 16) + (20) – 18 =
–64 + 64 + 20 – 18 = 2
So, the remainder is 2.
Answer 50
The correct answer is: $latex \text{x = }-\text{3} \pm \sqrt{5}$
For advanced algebra equations like this one, you need to complete the square.
STEP 1: Expand the equation to identify variables b and c.
Our equation x2 + 6x + 4 = 0 is in the format x2 + 2bx + c.
x2 + (2 × 3 × x) + 4 = x2 + 2bx + c
b = 3 and c = 4
STEP 2: Put the equation in the format (x + b)2 – b2 + c
(x + 3)2 – 32 + 4
STEP 3: Perform the operations to simplify.
(x + 3)2 – 32 + 4 = 0
(x + 3)2 – 9 + 4 = 0
(x + 3)2 – 5 = 0
(x + 3)2 – 5 + 5 = 0 + 5
(x + 3)2 = 5
STEP 4: Take the square root of each side and simplify to solve.
(x + 3)2 = 5
$ \sqrt{(x + 3)^2} = \pm \sqrt{5}$
$ \text{(x + 3) = } \pm \sqrt{5}$
$ \text{x + 3} – 3 = \pm \sqrt{5} – \text{3}$
$ \text{x = }-\text{3} \pm \sqrt{5} $
If you have had difficulties with these Accuplacer math prep problems, you may need to look at our pre-algebra review.
More Accuplacer Math Prep
